Generazione di numeri casuali
Richiami sulla teoria elementare dei sistemi.
Scopo dei numeri casuali
Un sistema si classifica come deterministico quando, sollecitandolo con una funzione di ingresso, si può determinare la sua evoluzione. Ad esempio, imprimendo ad un pallone una funzione Impulso di una certa durata (in questo caso l'impulso è di natura vettoriale, cioè ha un'intensità, un'inclinazione e un verso) si può prevedere la sua traiettoria, il punto di caduta, l'altezza massima raggiunta, per quanto tempo resta in volo, ecc.
Questa previsione si formula applicando le leggi della fisica.
I sistemi stocastici manifestano un comportamento regolato dal caso (dal greco stocas). Ad esempio il vento potrebbe introdurre una componente aleatoria che fa deviare il pallone dalla sua traiettoria.
Nella pratica, un generatore di numeri casuali trova applicazione nel campo dei giochi, delle simulazioni dei guasti ad una macchina, del dimensionamento di impianti basati sull'arrivo di richieste di servizio, ecc.
Ad esempio un commerciante che intende estendere la sua attività con l'offerta di nuovi servizi, ha necessità di valutare la convenienza del suo investimento. Potrebbe, a questo scopo, condurre un'indagine su un campione di clienti, per conoscere i gusti e le esigenze, quindi potrebbe simulare, conoscendo la frequenza con cui i suoi clienti lo visitano, quale frazione di essi potrebbe, potenzialmente, richiedere il nuovo servizio e, di conseguenza, dimensionare il nuovo reparto. Le richieste di servizio sono eventi casuali, che possono presentarsi in momenti imprevedibili.
Proprietà dei numeri casuali
Una sequenza di numeri casuali ha le seguenti proprietà:
la conoscenza di un numero della sequenza non consente di prevedere il prossimo numero che si presenterà, cioè, ogni numero della sequenza è indipendente dagli altri.
ogni numero della sequenza ha la stessa probabilità di presentarsi.
Per affidare al computer la generazione di numeri casuali si deve impiegare un algoritmo di generazione, quindi la prima proprietà non sarebbe soddisfatta, perchè conoscendo il metodo di generazione, diventa possibile prevedere la sequenza dei numeri. Per questa ragione i numeri generati con un algoritmo sono detti pseudo-casuali.
Generazione di numeri casuali.
Per simulare il verificarsi di un evento casuale occorre avere una sorgente che emetta dei valori casuali che riproducano una possibile successione di valori realmente osservabili. La base per costruire i vari comportamenti statistici è la variabile casuale distribuita uniformemente. Una variabile casuale x distribuita uniformemente è definita nel seguente modo:
(con k costante), cioè ogni numero ha la stessa probabilità k di essere estratto.
In termini pratici si ipotizza di disporre, all’interno di un’urna, di tutti i numeri reali compresi tra 0 e 1 (1 escluso). Si trova che nessun numero ha una preferenza di essere estratto rispetto agli altri, quindi, dopo un numero elevatissimo di estrazioni, ogni numero sarà stato scelto la stessa quantità di volte come gli altri. Il grafico p(x) di una distribuzione uniforme è una retta parallela all'asse delle ascisse, nell’intervallo [0, 1[ e la funzione non è definita all’esterno di tale intervallo.
metodo di Lehmer.
si basa sulla seguente relazione:
xn+1 = (a·xn + c) mod m
Cioè, dopo aver scelto un numero iniziale x0 della sequenza e, dopo aver fissato i valori delle costanti a, c ed m, si può ottenere un nuovo numero x1 calcolando il resto della divisione tra (a·x0 + c) ed m. Ricorsivamente si calcolano gli altri numeri x1, x2, …
Il divisore m è (preferibilmente) un numero primo che determina il periodo della sequenza. Sarebbe auspicabile riuscire ad ottenere tutti i numeri nell'intervallo [0, m-1]. A tale scopo sono stati individuati alcuni criteri per scegliere le costanti a e c:
la costante c non deve avere fattori in comune con m
ogni divisore primo di m deve dividere anche (a-1)
se m è multiplo di 4, deve esserlo anche (a-1)
Simulazione con Excel
Impostazione del foglio di calcolo
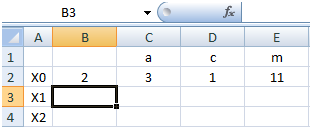
Nella prima riga sono state scritte le etichette che descrivono il significato dei valori della seconda riga: a=3, c=1, m=11. Questi valori assegnati alle costanti non soddisfano i criteri elencati prima.
Il valore nella cella B2 rappresenta il primo numero della sequenza x0, scelto in modo arbitrario.
Dall'applicazione della formula di Lehmer ci si aspetta di ottenere una sequenza di 11 numeri compresi tra 0 e 10.
Formula di Lehmer
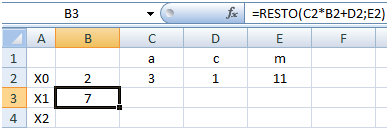
Nella cella B3 scrivere la formula di Lehmer: =RESTO(C2*B2+D2;E2).
Se si tenta di copiare la formula nelle celle B4-B20 si ottiene un errore.
Riferimenti relativi e riferimenti assoluti
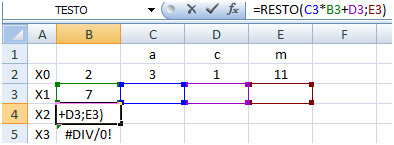
Per individuare l'errore, fare clic nella cella B4, poi fare clic nella barra della formula. Vengono evidenziate le celle riferite dalla formula. Si nota che questa formula fa riferimento a celle vuote, perchè le celle riferite dalla formula copiata si sono spostate insieme alla cella destinazione. Premere invio (o Esc) per uscire dalla barra della formula
Per bloccare le celle, fare clic sulla cella B3 e poi fare clic nella barra della formula, aggiungere il carattere dollaro davanti alla coordinata di riga 2, eccetto quella della cella B2.
Generazione della sequenza

Copiare la formula dalla cella B3 alle celle dell'intervallo B4:B20.
I valori in queste celle rappresentano la successione x1, x2, …
Si vede che sono stati generati solo 5 numeri diversi, prima che la sequenza si ripeta.
Se si modifica il valore x0, si cambiano solo i numeri della sequenza, se invece si cambia a e c si riesce ad ampliare l'intervallo.
Provare a=7 e c=3.
Condurre altri esperimenti con m = 17. Modificare le costanti a e c ed osservare i risultati.
La funzione CASUALE() di Excel.
Passare ad un nuovo foglio di lavoro.
In una cella qualsiasi scrivere la formula: =CASUALE(). Premere invio. Nella cella compare un numero casuale.
La funzione =CASUALE() genera numeri casuali compresi tra 0 e 1 (1 escluso).
Ogni volta che si scrive qualcosa in una cella viene generato un nuovo numero casuale.
Per generare un numero intero casuale nell'intervallo [a, b], si può usare la seguente formula:
=INT(CASUALE()*(b+1-a)) + 1
Ad esempio per generare numeri casuali compresi tra 1 e 90, la formula è: =INT(CASUALE()*90) + 1. Nel gioco della tombola, o anche in un gioco di carte, un numero estratto non viene rimesso nell'urna, quindi non compare fino a quando non si sono esauriti i numeri, mentre la funzione indicata potrebbe generare più volte lo stesso numero.
Esempio: lancio del dado.
la formula per generare un numero tra 1 e 6 è: =INT(CASUALE()*6) + 1
Scrivere la formula nella cella A1 e copiarla finmo alla cella A120. Cioè si simulano 120 lanci del dado.
Nelle celle da C1 a C6 scrivere i numeri che compaiono sulle facce del dado.
Nella cella D1 scrivere la formula per contare quante volte è stato estratto 1. Copiare la formula nelle celle D2:D6.

Ricalcolando le formule del foglio (con F9), si dovrebbe verificare che ogni valore del dado si presenta, in media, con la stessa frequenza, cioè 20 volte.
Lancio di due dadi

Simulare il lancio del secondo dado nelle celle B1:B120. Basta copiare l'intervallo A1:A120 nella cella B1. Nella cella C1 calcolare la somma dei punteggi dei dadi: =A1+B1. Copiare la formula nell'intervallo C2:C120.
I possibili risultati della somma delle facce dei dadi sono numeri compresi tra 2 e 12.
Calcolare la distribuzione di frequenza di questo risultato.
Qual è il valore più frequente e perchè.
Disegnare l'istogramma della Frequenza.
La funzione random() del Visual Basic for Application di Excel
Passare al Visual Basic Editor di Excel
Nel menu Inserisci (dell’editor di Visual Basic) scegliete Modulo
.Poi, ancora tramite il menu Inserisci, scrivere la routine Sub Dadi.
| |
Istruzione |
| 1 |
For i = 1 to 100 |
| 2 |
Cells(1, 1) = Int(Rnd() * 6) + 1 |
| 3 |
dado1 = Cells(1, 1) |
| 3 |
Cells(dado1 + 2, 2) = Cells(dado1 + 2, 2) + 1 |
| 3 |
Next |
Linea 1: Si suppone di lanciare il dado 100 volte.
Linea 2: Si genera un numero casuale compreso tra 1 e 6 e lo si scrive nella cella, del foglio attivo, in riga 1, colonna 1.
Linea 3: Il valore del dado viene scritto nella variabile Dado1.
Linea 4: Il valore del dado viene utilizzato come coordinata di riga per contare (nelle celle B3÷B8) il numero di volte che si è verificato questo valore.
L’istruzione descrive l’accesso ad un array bidimensionale. L’elemento riferito si trova nella riga ottenuta sommando 2 (perché si sono lasciate due righe vuote) al numero uscito sul dado.
Se è uscito 1 allora l’elemento si trova nella riga 3.
il secondo parametro dentro la parentesi (2) specifica la colonna 2 del foglio, cioè la colonna B.
il ciclo For termina con l’istruzione Next
Eseguire la macro numerose volte e verificare se i numeri hanno tutti la stessa frequenza. Lo si verifichi anche con un grafico.
Costruire l’istrogramma dei dati contenuti nell’intervallo B3:B8, assumendo come "Etichette asse categorie" l’intervallo A3:A8.
Eseguire la macro e osservare che l’uniformità della frequenza dei valori estratti non è proprio regolare ma i valori
sono comunque dello stesso ordine di grandezza.
Esercizi:
Per ognuna delle operazioni seguenti verificare il funzionamento del programma prima di passare alla successiva.
Simulare il lancio di due dadi mostrando, con un solo Message Box, i due numeri estratti.
Se i due numeri estratti sono diversi effettuare un altro lancio, se invece i due numeri sono uguali terminare il programma.
Chiedere al giocatore di tentare di indovinare il numero e, dopo il lancio, comunicare l’esito: Indovinato oppure sbagliato.
Se si inserisce un numero esterno all’intervallo [2, 12] bisogna ripetere la domanda del punto 3.
Contare il numero di lanci e il numero di risultati indovinati.
Terminare il programma se i numeri sui due dadi sono uguali oppure se si sono superati 20 tentativi.
Calcolare la percentuale di tentativi indovinati (Numero esiti indovinati / Lanci totali) e mostrarne il risultato.
soluzione: Lancio di 2 dadi
Lancio di 2 dadi
Con due dadi si possono ottenere i punteggi compresi tra 2 e 12.
Le probabilità dei singoli punteggi non sono più uguali tra loro. Infatti con due dadi si possono
presentare 36 casi, corrispondenti al prodotto dei 6 casi che si possono presentare su un dado e ai 6 casi che si possono abbinare sull'altro.
La probabilità che si ottenga il punteggio 2 quindi è 1/36, perchè dei 36 possibili abbinamenti dei punteggi sui singoli dadi, solo uno può
dare la somma 2: Uno sul primo e Uno sul secondo dado.
Per ottenere 3 ci sono 2 casi possibili: Uno sul primo dado e Due sul secondo e Viceversa. Quindi la probabilità di ottenere 3 è 2/36.
Per una spiegazione più dettagliata si può consultare un approfondimento.
La tabella seguente riepiloga le probabilità dei vari punteggi.
| Punteggio |
Probabilità |
| 2 |
1/36 |
| 3 |
2/36 |
| 4 |
3/36 |
| 5 |
4/36 |
| 6 |
5/36 |
| 7 |
6/36 |
| 8 |
5/36 |
| 9 |
4/36 |
| 10 |
3/36 |
| 11 |
2/36 |
| 12 |
1/36 |
Scegliere un intervallo del foglio, ad esempio A2:A12, ed inserirvi la numerazione da 2 a 12, corrispondente ai possibili punteggi che si possono ottenere sommando
i punti su ciascuna faccia del dado, dopo un lancio.
Scrivere la macro che simula il lancio dei due dadi e calcola la frequenza dei punteggi:
| Nr. riga |
Istruzione |
| 1 |
Sub DueDadi() |
| 2 |
For i = 1 To 100 |
| 3 |
dado1 = Int(Rnd() * 6 + 1) |
| 4 |
dado2 = Int(Rnd() * 6 + 1) |
| 5 |
somma = dado1 + dado2 |
| 6 |
Cells(somma, 2) = Cells(somma, 2) + 1 |
| 7 |
Next |
| 8 |
End Sub |
Esercizi:
Confrontare le probabilità attese (1/36, 2/36, …) con le frequenze ottenute.
Rappresentare l'istogramma della frequenza dei punteggi