Routing.

Algoritmi di instradamento

La tabella di instradamento contiene almeno due colonne: in una colonna contiene un indirizzo di rete e nell'altra colonna l'indirizzo dell'interfaccia collegata al canale che permette di raggiungere quella rete. Un pacchetto giunge in un router, il router legge l'indirizzo destinazione contenuto nell'header del pacchetto ed accede alla tabella di instradamento, alla ricerca della riga contenente l'indirizzo della rete a cui è destinato il pacchetto. Dalla seconda colonna determina il canale di uscita del pacchetto.

Gli algoritmi di instradamento, in esecuzione nei router della rete, si scambiano le informazioni per calcolare le tabelle.

Sia in una rete a datagramma, in cui i pacchetti di una stessa comunicazione possono seguire percorsi diversi, sia in una rete a circuito virtuale, dove i pacchetti di una stessa comunicazione seguono lo stesso percorso, il livello rete ha lo scopo di determinare il percorso che il pacchetto deve seguire per andare dal mittente al destinatario.

Nell'ambito di una sottorete, la commutazione è affidata alle stazioni, le quali leggono l'intestazione di livello 2 delle trame e usano l'indirizzo MAC per stabilire se sono o no destinatarie della trama. Gli indirizzi IP sono usati per scambiare pacchetti tra host residenti in sottoreti diverse (separate da router). Un host di una sottorete deve consegnare ad un router i pacchetti destinati ad un host appartenente ad un'altra sottorete. Questo router è denominato router di default. Anche l'host della sottorete di destinazione possiede un router di default.

Un algoritmo di instradamento deve determinare il percorso ottimale dal mittente al destinatario, attraverso la rete dei router. Per soddisfare questo criterio bisogna definire il costo del percorso, ovvero un insieme di variabili misurabili che si desidera che assumano un valore minimo. Il percorso ottimale è quello che ha il minimo costo. Il compito di determinare un cammino di costo minimo è complicato da alcune esigenze imposte dalle politiche di gestione delle reti. Ad esempio, un router X, di una organizzazione Y, potrebbe essere configurato per non instradare i pacchetti provenienti dalla rete di una organizzazione Z.

Per studiare i problemi di instradamento, una rete viene rappresentata con un grafo. Un grafo G=(N, E) è una coppia formata da un insieme di nodi N e un insieme di archi E che li congiungono. Nel contesto dell'instradamento in una rete, i nodi del grafo rappresentano i router, e gli archi rappresentano i canali che congiungono i router. La figura seguente mostra il grafo associato ad una rete.

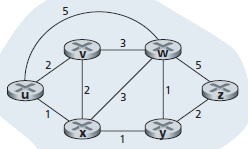
Nel grafo associato alla rete, accanto ad ogni arco c'è un numero che rappresenta il costo del cammino. Le variabili usate per quantificare il costo del cammino definiscono la metrica, ovvero i parametri per quantificare le proprietà del cammino. Alcuni parametri che si possono scegliere come metrica, sono ad esempio, la velocità del canale, il numero di router attraversati, la probabilità di errore sul canale, il ritardo medio causato dal traffico. Per il momento non ci si preoccupa di stabilire come viene determinato il costo di un canale.

Per ogni arco (x, y), che congiunge i nodi x e y, si indica con c(x, y) il costo del cammino tra x e y. Se però la coppia (x, y) non appartiene ad E, cioè non esiste un cammino diretto tra x e y, allora il costo viene indicato con c(x, y)=∞. In questo contesto, si considera che gli archi non siano orientati, cioè il costo del cammino da x a y è uguale al costo del cammino da y a x: c(x, y) = c(y, x). Un nodo y è adiacente ad un nodo x se la coppia (x, y)∈E.

Un algoritmo di routing ha lo scopo di individuare i percorsi di costo minimo tra un nodo e tutti gli altri. Per definizione, in un grafo G=(N, E), un cammino è una successione di nodi (x₁, x₂, …, x_p) tale che ogni coppia (x₁, x₂), (x₂, x₃), …, (x_p-1, x_p) è unita da un arco contenuto in E. Il costo del cammino (x₁, x₂, …, x_p) è la somma dei costi di tutti gli archi lungo il cammino, cioè c(x₁, x₂) + c(x₂, x₃) + ...+ c(x_p-1, x_p).

Comunque si scelgono due nodi x e y, esiste più di un percorso tra essi, e ogni cammino ha un costo. Tra questi ce ne sarà almeno uno di costo minimo.

Quindi il problema di un algoritmo di instradamento è quello di individuare il cammino di costo minimo tra una sorgente e una destinazione. Osservando la figura, per esempio, il cammino di costo minimo tra il nodo u e il nodo w è (u, x, y, w) con costo 3. Notare che se tutti gli archi nel grafo avessero lo stesso costo, il cammino di costo minimo, tra sorgente e destinazione, avrebbe anche il minimo numero di archi (canali).

Per esercizio trovare il percorso di costo minimo tra il nodo u e il nodo z del grafo mostrato in figura. Riflettere sul metodo applicato per scegliere tale percorso.

Probabilmente, dopo aver calcolato tutti i possibili percorsi (17) tra i due nodi, sono stati confrontati i costi e si è trovato il minimo.

Un calcolo simile è un esempio di algoritmo di routing centralizzato: in tale algoritmo, qualcuno, che conosce tutta la mappa della rete, si fa carico di calcolare il cammino tra una qualsiasi coppia di nodi e la comunica agli interessati.

Questa osservazione porta ad una prima classificazione degli algoritmi di routing in centralizzati e distribuiti.

Un algoritmo di routing centralizzato calcola il percorso di costo minimo tra una sorgente ed una destinazione, usando una conoscenza completa della rete. Cioè l'algoritmo deve ricevere, preliminarmente, in input le informazioni circa la raggiungibilità diretta di un nodo da parte di un altro nodo e il costo di quel canale di collegamento. Solo quando è in possesso di queste informazioni può procedere al calcolo. Il calcolo può essere eseguito da un unico computer a favore di tutti i router. L'efficacia di questo algoritmo ideale, è costituita dalle informazioni di input, cioè la conoscenza della mappa della rete e la conoscenza dei costi dei canali.
In un algoritmo di routing distribuito, il calcolo dei cammini di costo minimo viene eseguito dai nodi della rete, in modo iterativo. Inizialmente, ogni nodo della rete conosce solo i costi dei canali ai quali sono collegate le sue interfacce. Poi, attraverso un processo iterativo di scambio di informazioni con i suoi nodi adiacenti (cioè quelli che si trovano all'altra estremità del canale a cui è direttamente collegato), un nodo gradualmente calcola il cammino di costo minimo verso le altre destinazioni. Questo algoritmo di routing è detto Distance Vector perché ogni nodo memorizza, per ogni interfaccia, la stima dei costi (distanze) verso tutti gli altri nodi della rete.

Un'altra classificazione degli algoritmi di instradamento li distingue in statici e dinamici. Negli algoritmi statici, i percorsi tra una qualsiasi coppia di nodi cambiano raramente, per cui un amministratore interviene manualmente per modificare le tabelle di instradamento. Negli algoritmi dinamici, invece, tenendo conto delle variazioni della topologia, o dell'intensità del traffico, si deve provvedere ad aggiornare la tabella di instradamento. Questo aggiornamento può avvenire periodicamente, oppure, in conseguenza di una segnalazione relativa ad un costo variato. In quest'ultimo caso l'algoritmo si dice adattativo.

Un algoritmo adattativo, che riconosce variazioni nei costi dei canali e reagisce per ricalcolare la tabella di instradamento, soffre però di alcuni problemi. Ad esempio potrebbe creare dei cicli indesiderati nell'instradamento, e comunque potrebbe iterare lentamente prima di trovare una soluzione stabile.

Ancora un'altra classificazione degli algoritmi di instradamento riguarda la capacità di riconoscere l'intensità del traffico che porta alla congestione della rete. In questa metrica, si tiene conto di un parametro che varia dinamicamente. Se ad un canale congestionato si attribuisce un costo elevato, un algoritmo di routing tende a scegliere percorsi alternativi a quello congestionato. L'esperienza con le prime reti sperimentali ha evidenziato che prendere in considerazione il traffico di rete introduce nuove problematiche. La metrica usata dai moderni algoritmi di instradamento in Internet (RIP, OSPF, BGP) non tiene conto dell'intensità del traffico.

Algoritmi di routing di tipo Link State

In un algoritmo link-state, la topologia della rete e tutti i costi dei canali sono noti, cioè disponibili come input all'algoritmo LS. In pratica, ogni router invia un link-state packet a tutti gli altri router della rete. Un link-state packet contiene gli identificativi ed i costi dei canali a cui sono collegate le interfacce del router mittente. Come conseguenza della diffusione di questi pacchetti, ogni nodo della rete ha la stessa conoscenza complessiva della rete, cioè ogni router della rete conosce i router adiacenti di ogni altro router. Quindi ogni router può calcolare autonomamente lo stesso insieme di percorsi di costo minimo verso gli altri router.

L'algoritmo di Dijkstra assume che il nodo che sta calcolando i cammini di costo minimo verso tutti gli altri nodi della rete, sia la radice di una topologia ad albero. L'algoritmo di Dijkstra è iterativo, ed ha la proprietà che dopo k iterazioni ha calcolato i percorsi di costo minimo verso k nodi destinazione, e tra tutti i percorsi di costo minimo, verso tutte le destinazioni, questi k cammini hanno i k costi più piccoli.

Si introduca la seguente notazione

D(v): costo del cammino di costo minimo tra un nodo sorgente ed un nodo destinazione v alla iterazione corrente dell'algoritmo.
p(v): nodo precedente (adiacente a v) lungo il cammino dalla sorgente al nodo v.
N: sottoinsieme di nodi; v è contenuto in N se il percorso dalla sorgente a v è stato determinato completamente.

L'algoritmo consiste di una fase di inizializzazione seguita da un ciclo. Il numero di cicli eseguiti è uguale al numero di nodi della rete. Al termine, l'algoritmo ha calcolato tutti i percorsi di costo minimo tra la sorgente u e tutti gli altri nodi della rete.

Algoritmo di Dijkstra svolto dal nodo u

1 Inizializzazione:
2   N' = {u}
3   per tutti i nodi v
4     se v è adiacente a u
5       then D(v) = c(u,v)
6       else D(v) = ∞
7
8 Loop
9    trovare un nodo w non contenuto in N' tale che D(w) è un minimo
10   aggiungere il nodo w a N'
11   aggiornare D(v) per ogni vicino v di w non contenuto in N':
12     D(v) = min(D(v), D(w) + c(w,v))
13 /* il nuovo costo verso v è rimasto uguale oppure si è trovato 
14    un percorso di costo minore dato dal costo verso w più il costo da w a v

15 until N'= N

Ad esempio, si calcolino i cammini di costo minimo dal nodo u verso tutti gli altri nodi della rete mostrata nella figura precedente.

La tabella seguente mostra, in ciascuna riga, i valori delle variabili alla fine di ogni passaggio del ciclo.

passo	N'	D(v), p(v)	D(w), p(w)	D(x), p(x)	D(y), p(y)	D(z), p(z)
0	u	2, u	5, u	1, u	∞	∞
1	ux	2, u	4, x		2, x	∞
2	uxy	2, u	3, y			4, y
3	uxyv		3, y			4, y
4	uxyvw					4, y
5	uxyvwz

Il dettaglio dei primi passi:

nel passo di inizializzazione, ai percorsi di costo minimo, attualmente noti, da u ai suoi adiacenti v, x, e w vengono assegnati i valori 2, 1 e 5. Notare che al costo verso w è assegnato il valore 5, nonostante ci sia un percorso migliore. Il valore 5 è il costo del cammino diretto (1 hop) da u a w. Ai costi dei cammini per raggiungere y e z viene assegnato il valore infinito, perché questi nodi non sono direttamente connessi a u.
Nella prima iterazione, si cercano i nodi, non ancora aggiunti all'insieme N', con il costo minimo. Cioè il nodo x, con costo 1, che viene aggiunto all'insieme N'. A questo punto si aggiorna D(v) per tutti i nodi v, e si ottengono i risultati mostrati sulla riga della tabella, in corrispondenza del passo 1. Il costo del percorso verso v resta invariato. Il costo del percorso verso w (che era 5) attraverso il nodo x diventa 4. Quindi si è trovato un percorso di costo minore. Il nodo precedente di questo nodo w, lungo questo cammino di costo minore da u, è il nodo x. Analogamente, il costo verso y, attraverso x è 2.
Nella seconda iterazione, si trova che i nodi v e y hanno i percorsi di costo minimo (2), si aggiunge y all'insieme N', così che N' adesso contiene u, x e y. Il costo dei nodi restanti non ancora contenuti in N', cioè i nodi v, w, e z, vengono aggiornati, ottenendo i risultati mostrati nella riga corrispondente al passo 2.
Nella seconda iterazione, si trova che i nodi v e y hanno i percorsi di costo minimo (2), e si aggiunge il nodo y all'insieme N'. Adesso N' contiene i nodi: u, x, e y. Si ricalcolano e si aggiornano i costi verso i restanti nodi non ancora in N', cioè i nodi v, w, e z, ottenendo i risultati mostrati nella riga corrispondente al passo 3.
…

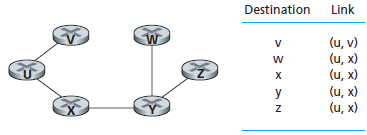
Quando l'algoritmo Link State termina, sono stati trovati, per ogni nodo, tutti i precedenti lungo il cammino di costo minimo che parte dal nodo sorgente. Quindi si può ricostruire, a ritroso, il percorso da tutti i destinatari alla sorgente. La tabella di instradamento in un nodo, ad esempio u, può essere calcolata da queste informazioni memorizzando, per ogni destinazione, il nodo successivo alla sorgente u che nel cammino di costo minimo porta alla destinazione. Il risultato dell'algoritmo di Dijkstra è una topologia ad albero estratta dalla topologia a maglia (Spanning Tree).

Qual è la complessità del calcolo? Cioè dati n nodi (non contando la sorgente), quanti calcoli sono necessari nel caso peggiore per trovare tutti i percorsi di costo minimo dalla sorgente verso tutte le destinazioni? Nella prima iterazione è necessario visitare tutti i nodi per trovare il nodo w non presente in N' che ha il costo minimo. Nella seconda iterazione, si devono visitare n-1 nodi per determinare il percorso di costo minimo, nella terza iterazione si devono visitare n-2 nodi e così via. In totale al termine di tutte le iterazioni sono stati visitati n·(n-1)/2 nodi, per n molto grande 1 diventa trascurabile, quindi l'algoritmo LS ha una complessità dell'ordine di n², che si indica con O(n²).

Quando si è vicini alla congestione, l'algoritmo Link State può modificare frequentemente la tabella di instradamento. Nella figura seguente i costi dei canali sono misurati sulla base del traffico, ad esempio, osservando i ritardi tra i pacchetti che hanno la stessa provenienza. In questo esempio i costi dei canali non sono simmetrici, cioè c(u, v) = c(v, u) solo se il traffico sul canale tra u e v, in entrambe le direzioni, è lo stesso. Nell'esempio, il nodo z genera un traffico destinato a w, di intensità unitaria, il nodo x genera un traffico di intensità unitaria destinato a w e il nodo y immette un traffico di intensità e, anche questo destinato a w. Nella figura A è mostrato il routing iniziale, dove i costi dei canali riguardano il taffico sul canale. Quando, in seguito, verrà rieseguito l'algoritmo Link State, il nodo y determina, sulla base dei costi noti (fig. A) che il percorso in senso orario verso y ha costo 1, mentre il percorso in senso antiorario a w ha costo 1+e.

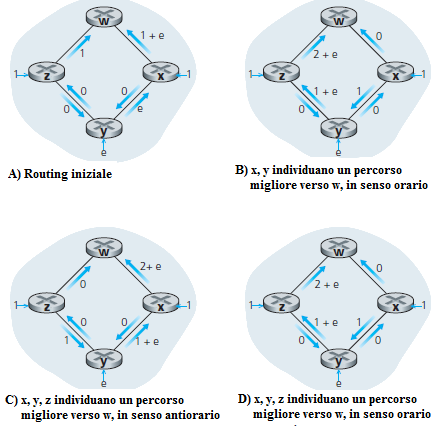
Quindi il cammino di costo minimo verso w, adesso è quello in senso antiorario. Analogamente, x determina che il suo nuovo cammino di costo minimo verso w è quello in senso orario , con i costi mostrati in figura B).

Alla successiva esecuzione dell'algoritmo Link State, i nodi x, y e z individuano un percorso di costo 0 verso w in senso antiorario, e tutti instradano il traffico sul cammino in senso antiorario. Il caso descritto è un problema che si manifesta con qualsiasi algoritmo di instradamento, non solo con il Link State. Si verificano oscillazioni nel traffico quando tra i parametri della metrica si sceglie il ritardo dei pacchetti che hanno la stessa provenienza o, comunque, una indicazione relativa allo stato di congestione di un canale. Una soluzione dovrebbe essere quella di non calcolare i costi dei canali in funzione del traffico. Ma è inaccettabile, perché un instradamento ha anche lo scopo di non intasare ulteriormente un canale congestionato (sul quale si notano elevati ritardi). Un'altra soluzione potrebbe essere quella di obbligare i router a non eseguire l'algoritmo di instradamento contemporaneamente, basterebbe eseguire l'algoritmo di instradamento con una periodicità diversa tra tutti i router, ad esempio, generando un tempo casuale dopo cui il router invia i pacchetti di servizio (Link State Packet).

Algoritmo di instradamento Distance Vector

L'algoritmo Link State è adattativo e ogni router ha una conoscenza completa della rete, l'algoritmo Distance Vector è iterativo, distribuito, asincrono. È distribuito perché ogni nodo riceve le informazioni solo dai suoi vicini, a cui è direttamente collegato, esegue i calcoli e distribuisce i risultati ai suoi vicini. È iterativo perché il processo di distribuzione continua fino a quando termina lo scambio di informazioni tra i vicini. L'algoritmo è asincrono perché non si richiede che i router operino rispettando vincoli di temporizzazione o di transizioni di stato.

Prima di descrivere in dettaglio l'algoritmo Distance Vector, è utile osservare che esite una relazione tra i cammini di costo minimo. Si indichi con d_x(y) la lunghezza del cammino di costo minimo dal nodo x al nodo y (la lettera d usata in questo contesto, è l'iniziale di distanza temporale). Mentre con c(x, v) si intende il costo del cammino da un nodo x al nodo adiacente v.

L'equazione di Bellman-Ford stabilisce:

d_x(y) = min_v{c(x, v) + d_v(y)}

Dove min_v è esteso a tutti i vicini di x.
L'equazione di Bellman-Ford asserisce che, dopo aver viaggiato da x a v, se si prende il percorso di costo minimo da v a y, il costo complessivo del cammino è c(x, v) + d_v(y). Ogni nodo x conosce il costo per raggiungere ciascuno dei suoi vicini v, allora il minimo costo da x a y è il minimo tra tutti i c(x, v) + d_v(y) (cioè calcolato per tutti i vicini v).

Per verificare la validità dell'equazione di Bellman-Ford, si effettui il calcolo per il nodo sorgente u e il nodo destinazione z in figura.

Il nodo sorgente u ha tre vicini: i router v, x e w. Ci sono vari cammini che, da ciascuno di questi vicini, raggiunge z, i costi dei cammini ottimali sono: d_v(z) = 5, d_x(z) = 3, e d_w(z) = 3 Inserendo questi valori nell'equazione di Bellman-Ford insieme con i costi c(u, v) = 2, c(u, x) = 1, e c(u, w) = 5, si ottiene:

d_u(z) = min{2 + 5, 5 + 3, 1 + 3} = 4

che conferma la validità dell'equazione di Bellman-Ford, ed è lo stesso risultato ottenuto applicando l'algoritmo di Dijkstra.

L'importanza dell'equazione di Bellman-Ford nella pratica è che essa fornisce le righe della tabella di instradamento di un nodo x. Infatti sia v* un qualsiasi nodo, adiacente a x, per cui vale il minimo nell'equazione di Bellman-Ford. Se il nodo x vuole inviare un pacchetto al nodo y lungo il percorso di costo minimo, dovrebbe consegnare il pacchetto al nodo v*. Quindi la tabella di instradamento del nodo x dovrebbe specificare che il nodo v* è il nodo Next-Hop che consente di raggiungere la destinazione finale y.

Un'altra importante applicazione pratica dell'equazione di Bellman-Ford è che essa suggerisce quale forma di comunicazione tra router adiacenti deve avvenire nell'algoritmo Distance Vector.

L'idea è la seguente. Si indichi con N l'insieme dei nodi della rete e si indichi con D_x = {D_x(y): y ∈ N} il Distance Vector del nodo x, cioè il vettore dei costi da x verso tutti gli altri nodi y contenuti in N. Ogni nodo x assegna un valore a D_x(y), come una stima del costo del cammino di costo minimo da sé stesso verso y, per tutti i nodi y in N.

Per applicare l'algoritmo Distance Vector, ogni nodo possiede le seguenti informazioni di instradamento:

il costo c(x, v) da x al vicino v (direttamente collegato), per ogni vicino v.
il Distance Vector del nodo x, cioè D_x = {D_x(y): y ∈ N} contenente i valori dei costi verso tutte le destinazioni y contenute in N.
i Distance Vector di ciascuno dei suoi vicini, cioè D_v = {D_v(y): y ∈ N} per ogni vicino v di x.

Nell'algoritmo distribuito e asincrono, periodicamente, ogni nodo invia una copia del suo Distance Vector a tutti i router adiacenti. Quando un router x riceve un nuovo Distance Vector da uno dei suoi vicini v, salva il Distance Vector di v ed applica l'equazione di Bellman-Ford per aggiornare il suo Distance Vector:

D_x(y) = min_v{c(x, v) + D_v(y)} per ogni nodo y in N

Se dopo questo calcolo, il Distance Vector di x è diverso da quello già memorizzato, il nodo x invia il suo Distance Vector aggiornato a tutti i suoi vicini, che, a loro volta, usano per aggiornare i propri Distance Vector. I nodi continuano il processo di comunicazione di un Distance Vector modificato in modalità asincrona. Ad un certo punto ogni costo D_x(y) converge a d_x(y), il costo corrente del percorso di costo minimo dal nodo x al nodo y.

Algoritmo Distance Vector

Per ogni nodo x:

1 Inizializzazione:
2 per tutte le destinazioni y in N:
3   D_x(y) = c(x, y) /* se y non è adiacente allora c(x, y) = ∞ */
4 per ogni vicino w
5   D_w(y) = ? per tutte le destinazioni y in N
6 per ogni vicino w
7   invia a w il Distance Vector D_x = {D_x(y): y ∈ N} 
8
9 loop
10   wait (evento "è cambiato il costo del canale verso un certo vicino w" oppure
11              "si riceve un Distance Vector da un certo vicino w")
12
13 per ogni y in N:
14   D_x(y) = min_v{c(x, v) + D_v(y)}
15
16 se D_x(y) è cambiato per qualche destinazione y
17   invia a tutti i vicini il Distance Vector D_x = {D_x(y): y in N}
18
19 forever

Nell'algoritmo Distance Vector, un nodo x ricalcola il Distance Vector in seguito al verificarsi di uno tra due eventi possibili. Il nodo vede che il costo di un canale che lo congiunge ad un suo vicino è cambiato, oppure il nodo riceve, da un suo vicino, un Distance Vector diverso da quello precedentemente memorizzato. Ma per aggiornare la sua tabella di instradamento per una data destinazione y, il nodo x non ha bisogno di conoscere la distanza più breve verso y, ma deve conoscere il nodo v*(y) (Next Hop) che si trova sul cammino ottimale verso y. Il router Next Hop, v*(y), è il vicino v che soddisfa il requisito del costo minimo calcolato nella linea 14 dell'algoritmo DV. Potrebbero esserci più nodi v che danno un minimo, in questo caso è indifferente quale viene scelto. Nelle linee 13 e 14, per ogni destinazione y, il nodo x determina v*(y) e aggiorna la sua tabella di instradamento per la destinazione y.

L'algoritmo Link State esige che ogni nodo abbia una conoscenza completa della mappa della rete prima prima di applicare l'algoritmo di Dijkstra. L'algoritmo Distance vector, è distribuito, non usa queste informazioni globali. La sola informazione che un nodo deve avere è il costo di ciascun canale. Il nodo riceve questa informazione dai propri vicini. Ogni nodo resta in attesa di ricevere un aggiornamento dai suoi vicini (linee 10 e 11), calcola il suo nuovo Distance Vector quando riceve un aggiornamento (linea 14) e diffonde il suo nuovo Distance Vector ai suoi vicini (linee 16 e 17).

I protocolli di routing RIP e BGP in Internet usano l'algoritmo Distance Vectori.

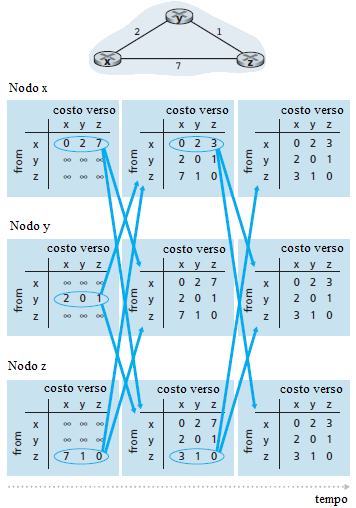
La figura precedente illustra le operazioni dell'algoritmo Distance Vector per la rete formata da tre nodi della figura. Si ipotizza un funzionamento sincrono, in cui tutti i nodi della rete ricevono contemporaneamente i Distance Vector dai loro vicini, calcolano il loro nuovo Distance Vector e lo comunicano ai loro vicini se risultano diversi da quelli già memorizzati.

Ci si dovrebbe convincere che l'algoritmo converge verso uno stato di stabilità anche se i Distance Vector vengono comunicati in momenti diversi.

Nella colonna di sinistra della figura, sono mostrate le tabelle di routing iniziali, per ciascuno dei tre nodi. In una tabella di instradamento, ciascuna riga è una distanza, più esattamente, ogni tabella di instradamento di un router contiene il suo Distance Vector e quelli dei suoi vicini. La prima riga nella tabella di instradamento iniziale del nodo x è D_x = {D_x(x), D_x(y), D_x(z)} = {0, 2, 7}. la seconda e la terza riga, in questa tabella, sono gli ultimi Distance Vector ricevuti. dai nodi y e z. Siccome all'inizio, il nodo x non ha ricevuto nessuna informazione dai nodi y e z, a queste due righe vengono assegnati i valori infinito.

Dopo l'inizializzazione, ogni nodo invia il suo Distance Vector a ciascuno dei due vicini. Nella figura, questa comunicazione è indicata con le frecce che partono dalla prima colonna e giungono nella seconda. Ad esempio, il nodo x invia il suo Distance Vector D_x = {0, 2, 7} ai nodi y e z. Dopo aver ricevuto gli aggiornamenti, ciascun nodo ricalcola il proprio Distance Vector.

Ad esempio, il nodo x ricalcola:

D_x(x) = 0
D_x(y) = min{c(x, y) + D_y(y), c(x, z) + D_z(y)} = min{2 + 0, 7 + 1} = 2
D_x(z) = min{c(x, y) + D_y(z), c(x, z) + D_z(z)} = min{2 + 1, 7 + 0} = 3

Quindi la seconda colonna mostra, per ogni nodo, il nuovo Distance Vector del nodo insieme con i Distance Vector appena ricevuti dai vicini. Notare, ad esempio, che il nodo x stima che il costo minimo verso il nodo z, D_x(z), è cambiato da 7 a 3. Inoltre, per il nodo x, il nodo adiacente y soddisfa il requisito del minimo indicato nella linea 14 dell'algoritmo Distance Vector. Quindi in questa fase dell'algoritmo, nel nodo x si ha v*(y) = y e v*(z) = y.

Dopo che i nodi hanno ricalcolato i loro Distance Vector, inviano i Distance Vector aggiornati a tutti i vicini, se sono diversi dai precedenti. Questo, nella figura, corrisponde alle frecce che dalla seconda colonna giungono nella terza.

Notare che solo i nodi x e z inviano aggiornamenti: il Distance Vector del nodo y non è cambiato così che il nodo y non invia un aggiornamento. Dopo la ricezione di un aggiornamento, i nodi calcolano i loro Distance Vector ed aggiornano la tabella di instradamento, come mostrato nella terza colonna della figura.

Il processo di ricezione dei Distance Vector dai propri vicini, il ricalcolo delle righe della tabella di instradamento e la trasmissione ai vicini delle variazioni dei costi del percorso di costo minimo verso una destinazione, continua fino a quando non ci sono più scambi di informazioni di stato. A questo punto, poiché non ci sono messaggi di aggiornamento, non avviene nessun ricalcolo della tabella di instradamento e i nodi passano nello stato di attesa (linee 10 e 11). L'algoritmo resta in questo stato fino a quando si verifica uno degli eventi specificati.

Esempio di applicazione dell'algoritmo Distance Vector

Variazioni dei costi e interruzioni di un canale.

Durante l'esecuzione dell'algoritmo Distance Vector, un nodo che rileva una variazione del costo di un canale da sé stesso ad un vicino (linee 10 e 11), aggiorna il suo Distance Vector (linee 13 e 14) e, se il costo del percorso di costo minimo risulta cambiato, invia il nuovo Distance Vector ai suoi vicini.

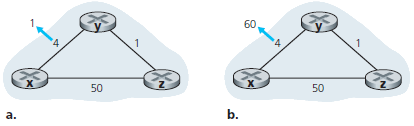
La figura a. mostra un esempio in cui il costo del canale da y a x cambia da 4 a 1. In questo momento interessano solo le righe dei Distance Vector di y e di z verso la destinazione x. Si verificano i seguenti eventi:

Al tempo t₀, y rileva una variazione del costo del canale (il costo è cambiato da 4 a 1), aggiorna il suo Distance Vector, e lo comunica ai suoi vicini.
Al tempo t₁, z riceve l'aggiornamento da y e ricalcola la sua tabella. Calcola un nuovo costo minimo verso x (è diminuito da un costo 5 a un costo 2) ed invia il suo nuovo Distance Vector ai suoi vicini.
Al tempo t₂, y riceve un aggiornamento da z e modifica il suo Distance Vector. I costi minimi di y non cambiano e quindi y non invia il Distance Vector a z e l'esecuzione dell'algoritmo passa in uno stato di attesa.

Così, dopo due iterazioni l'algoritmo Distance Vector ha raggiunto uno stato stabile. Un miglioramento della tabella di instradamento si è propagato sulla rete, ma cosa succede se il costo di un canale cresce? Ad esempio (figura b.) il costo del canale tra x e y cresce da 4 a 60.

Prima che il costo del canale cambi:
D_y(x) = 4,
D_y(z) = 1,
D_z(y) = 1,
D_z(x) = 5.
Al tempo t₀, y riconosce una variazione del costo del canale che lo collega a x (passa da 4 a 60). Di conseguenza y calcola che il nuovo cammino di costo minimo verso x ha il costo:
D_y(x) = min{c(y, x) + D_x(x), c(y, z) + D_z(x)} = min{60 + 0, 1 + 5} = 6
Osservando la rete, si nota che questo nuovo costo attraverso z è sbagliato. Ma la sola informazione che ha il nodo y è che il costo lungo il cammino diretto a x è 60 e che z aveva informato y che poteva raggiungere x con costo 5. Quindi, per raggiungere x, y cerca di passare attraverso z, ritenendo che da qui si possa poi giungere a x con costo 5. Al tempo t₁ si crea un instradamento ciclico: per raggiungere x, y consegna i pacchetti a z e z li consegna a y. Un instradamento ciclico è come un buco nero (la luce che entra non esce più): un pacchetto destinato a x che giunge a y oppure a z, verrà riflesso da un nodo all'altro per sempre (o fino a quando cambiano le tabelle di instradamento).
Il nodo y, che ha calcolato un nuovo costo minimo verso x, invia il nuovo Distance Vector a z al tempo t₁.
In un istante successivo a t₁, z riceve il nuovo Distance Vector di y, che indica che il costo minimo verso x è 6. Il nodo z sa che può raggiungere y con costo 1 e quindi calcola un nuovo costo minimo verso x:
D_z(x) = min{50 + 0,1 + 6} = 7
Poiché il costo minimo che z incontra verso x è aumentato, z informa y del suo nuovo Distance Vector al tempo t₂.
Analogamente, dopo aver ricevuto il Distance Vector di z, y determina D_y(z) = 8 ed invia a z il suo Distance Vector. Il nodo z determina D_z(x)=9 e invia ad y il suo nuovo Distance Vector, e così via.

Si verificheranno 44 cicli (messaggi scambiati tra y e z), fino a quando z calcola che il costo del cammino attraverso y è maggiore di 50. A quel punto, z si accorge che il suo percorso di costo minimo verso x è quello attraverso il canale direttamente collegato a x. Il nodo y, quindi, instraderà i pacchetti destinati a x, attraverso il nodo z. I peggioramenti della rete (il costo di un canale è aumentato) si propagano lentamente. Cosa sarebbe successo se il costo del canale c(y, x) fosse cambiato da 4 a 10.000 e il costo c(z, x) fosse diventato 9.999? Questa situazione è denominata "il problema del conteggio a infinito".

Poisoned Reverse

Il ciclo che è stato descritto, può essere evitato con la tecnica poisoned reverse. L'idea è: se z cerca di raggiungere la destinazione x attraverso y, allora z avvertirà y che la sua distanza verso x è infinita, cioè z dirà a y che D_z(x)=∞ (anche se sa che, in realtà, D_z(x)=5). Il nodo z continuerà a dire questa bugia a y, fintantoché invia ad y i pacchetti da consegnare a x. A questo punto il nodo y ritiene che z non ha nessun altro percorso da scegliere per raggiungere x, quindi y non tenterà mai di raggiungere x attraverso z, per tutti i pacchetti provenienti da z e diretti a x.

La tecnica poisoned reverse risolve il problema del ciclo visto nella figura b. Infatti avendo posto D_z(x)=∞, quando il costo del canale (x, y) cambia da 4 a 60, al tempo t₀, y aggiorna la sua tabella e continua ad instradare direttamente a x, sebbene il costo sia 60, ed informa z del suo nuovo costo verso x, Cioè D_y(x)=60. Dopo aver ricevuto l'aggiornamento al tempo t₁, z immediatamente sostituisce la riga corrispondente all'instradamento verso x con la nuova riga che indica il canale diretto (x, z) al costo 50. Poiché questo è un nuovo cammino di costo minimo verso x, e visto che non passa più attraverso y, il nodo z, al tempo t₂, informa y che D_z(x)=50. Dopo aver ricevuto l'aggiornamento da z, y aggiorna il suo Distance Vector con D_y(x)=51. Inoltre, poiché adesso z si trova sul cammino di costo minimo verso x, y avvelena il percorso a ritroso da z a x, informando, al tempo t₃, il nodo z che D_y(x) = ∞ (anche se y sa che in realtà D_y(x)=51.

La tecnica del poisoned reverse non risolve il problema del conteggio all'infinito. Se il ciclo interessa tre o più nodi (non solo due nodi adiacenti) non viene individuato dalla tecnica poisoned reverse.

Confronto tra gli algoritmi DV e LS

I due algoritmi Distance Vector e Link State assumono un approccio complementare per il calcolo della tabella di instradamento. Nel Distance Vector ogni nodo informa solo i suoi nodi adiacenti, ma ad essi fornisce un riassunto dei percorsi di costo minimo da sé stesso verso tutti gli altri nodi che conosce. Nell'algoritmo Link State, ogni nodo invia a tutti gli altri nodi (in broadcast) solo il costo dei cammini verso i suoi vicini.

In conclusione, ricordando che N è l'insieme dei nodi (router) ed E è l'insieme degli archi (canali):

Complessità. Il Link State richiede che ogni nodo conosca il costo di ciascun canale della rete, quindi sono necessari N·E messaggi. Inoltre, quando il costo di un canale cambia, il nuovo costo deve essere comunicato a tutti i nodi. L'algoritmo Distance Vector richiede uno scambio di messaggi solo tra i nodi adiacenti. Il tempo di calcolo dipende da molti fattori. Quando il costo di un canale cambia, l'algoritmo Distance vector propaga l'informazione solo se il nuovo costo produce un nuovo cammino di costo minimo verso uno dei nodi direttamente collegato a quel canale.
Velocità di convergenza. L'algoritmo Link State ha una complessità dell'ordine di N². L'algoritmo Distance Vector converge lentamente e può creare dei cicli di instradamento. Il Distance Vector è anche soggetto al problema del conteggio all'infinito.
Robustezza. Se un router subisce un guasto o un sabotaggio, con l'algoritmo Link State il router invia in broadcast un costo errato per uno dei suoi canali direttamente collegati, ma non di altri. Un nodo potrebbe anche alterare o scartare qualche pacchetto di brodcast ricevuto. Ma un nodo calcola solo la propria tabella di instradamento, gli altri nodi eseguono lo stesso calcolo per sé stessi. Questo significa che i calcoli sono separati e quindi assicurano una certa robustezza. Con l'algoritmo Distance Vector, un nodo può inviare informazioni sbagliate, relative ai percorsi di costo minimo, a una o più destinazioni.

Non esistono quindi motivi che permettono di privilegiare uno dei due algoritmi. In Internet sono usati entrambi.

Altri algoritmi di instradamento

Prima che in Internet si affermassero i due algoritmi di instradamento Link State e Distance Vector, esistevano altri algoritmi di instradamento. Una classe di algoritmi si basava sull'osservazione del traffico tra le sorgenti e le loro destinazioni. Matematicamente era un problema di ottimizzazione con vincoli. Un'altra classe di algoritmi di instradamento derivava dall'esperienza nel mondo della telefonia. Gli algoritmi applicati nella rete a commutazione di circuito venivano usati anche nelle reti digitali a commutazione di pacchetto, nei casi in cui le risorse (buffer, frazione di banda), per ogni canale, venivano assegnate alle comunicazioni che viaggiavano su quel canale.