Trasduttori

definizione.

Un trasduttore è un dispositivo che converte una grandezza fisica in un'altra

Introduzione.

Un uomo percepisce le informazioni provenienti dall'ambiente in cui si trova servendosi dei suoi organi di senso; il cervello acquisisce tali informazioni e, eventualmente, produce una serie di azioni. In natura esistono informazioni che si presentano sotto una forma non decodificabile dai sensi, ad esempio una direzione geografica, un ultrasuono, una radioattività sono grandezze che per poter essere acquisite devono essere trasformate in una forma riconoscibile da uno dei sensi. Quest'operazione viene eseguita dai 'sensi artificiali' detti trasduttori.

Principio di funzionamento.

Un trasduttore è un dispositivo nel quale l'azione di una grandezza fisica esterna, di una certa natura, provoca una trasformazione di una proprietà fisica del dispositivo stesso, che viene usata per risalire all'entità dell'azione esterna; un trasduttore, cioè, rende osservabile una grandezza fisica.

Questa definizione identifica come trasduttore un qualsiasi oggetto che stabilisce un'associazione univoca tra lo stimolo che esso subisce dall'esterno, e la relativa modificazione, che può essere osservata misurando una sua proprietà. Per i nostri scopi interessano i trasduttori che forniscono una misura di tipo elettrico. Tale associazione deve conservarsi nel tempo e nello spazio, ovvero la misura di un certo stimolo deve essere sempre la stessa in ogni luogo e in ogni momento. La misura non deve essere distruttiva ma ripetibile, cioè verificabile.

L'interesse per i trasduttori deriva dalla capacità, che essi offrono, di poter affidare ad un elaboratore compiti che per un operatore umano potrebbero risultare svantaggiosi o rischiosi. Un operatore che controlla un processo osserva con continuità gli strumenti di misura che indicano lo stato dei vari componenti coinvolti e interviene per regolare certe variabili. Un simile controllo è inadeguato perchè: l'operatore si stanca, si distrae, ha un tempo di reazione a volte lungo e potrebbe anche operare in condizioni di rischio. Il punto di vista dell'automazione prevede di rimpiazzare l'ipotetico operatore addetto al controllo del processo, con un elaboratore che acquisisce informazioni da trasduttori e governa i meccanismi atti a svolgere il compito in un modo rapido e sicuro, e di trasferire all'uomo mansioni più gratificanti.

Tutti gli strumenti di misura sono esempi di trasduttori:

il termometro converte la temperatura del corpo, con cui entra in intimo contatto, in una lunghezza (altezza del mercurio nella colonnina);
il Tachimetro converte una velocità angolare nell'angolo di rotazione descritto dalla lancetta.

Il principio di funzionamento di un trasduttore si basa sul fatto che un certo dispositivo è sensibile ad una certa sollecitazione, manifestando questa sensibilità con l'alterazione di una qualche sua proprietà fisica. La tabella seguente riepiloga i fenomeni che si verificano in alcuni trasduttori e le grandezze associate:

Trasduttore	Grandezza da misurare	Fenomeno	Grandezza fisica alterata
Termometro	Temperatura	dilatazione termica	altezza del mercurio
Tachimetro	Velocità	Induzione elettromagnetica	angolo di rotazione della lancetta
Bilancia	Peso	Momento meccanico	coppia antagonista di equilibrio
Cronometro	Tempo	Oscillazioni	numero di periodi

La misura della grandezza fisica alterata (lunghezza, resistenza, ecc.) permette di risalire, tramite la conoscenza della legge che descrive il fenomeno, alla grandezza incognita.

Esempio: Se si conosce la legge che descrive il fenomeno, la misura della grandezza fisica alterata nel trasduttore consente di risalire al valore della grandezza incognita.

Infatti se si sa che un materiale possiede un coefficiente di dilatazione termica λ di 5·10^-3 mm/°C, e si ha una barretta che a 0°C misura 50 mm in lunghezza, allora quando la sua lunghezza diventa 50.5 mm, si può calcolare che la temperatura dell'ambiente in cui è immersa vale 100°C.

È noto che la lunghezza L di una lamina metallica dipende dalla temperatura T a cui viene portata. Ammettendo che esista una relazione di proporzionalità tra la dilatazione e la temperatura, si ha:

L - L₀ = λ · (T - T₀)

In cui L è la lunghezza della lamina a temperatura T e L₀ è la lunghezza della lamina a temperatura T₀. Quindi ponendo T₀ = 0 °C, misurando la dilatazione L-L₀ della lamina è possibile calcolare la temperatura T:

T = $\frac{{L -L}_{0}}{λ}$

che, con i valori ipotizzati, fornisce:

T = 0.5 / 5·10^-3 = 100°C.

Nel trasduttore di temperatura, la temperatura è lo stimolo che produce, come trasformazione delle proprietà fisiche del trasduttore, la variazione della lunghezza della lamina. Quindi la temperatura è la variabile di ingresso e la lunghezza della lamina è la variabile di uscita. Il modello matematico del sistema è:

T = $\frac{{L -L}_{0}}{λ}$ + T₀

Cioè, se si può misurare la lunghezza della lamina e si conosce il suo coefficiente di dilatazione termica, si può risalire alla temperatura a cui è sottoposto il trasduttore.

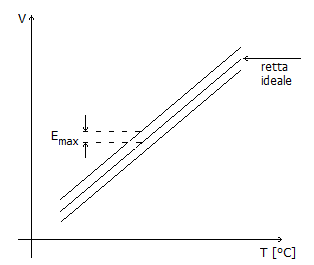
La rappresentazione grafica del modello matematico del trasduttore viene ottenuta riportando sull'asse delle ascisse i valori della variabile di ingresso e sull'asse delle ordinate i valori della variabile di uscita. Il risultato è una retta, detta anche retta ideale perchè lungo essa dovrebbero disporsi tutte le misure.

Retta ideale: le misure che si dispongono lungo questa retta sono prive di errori. Corrispondono al vero valore della grandezza da misurare

Rette del minimo e del massimo errore: delimitano la regione di valori entro cui cadono le misure che, per disturbi imprevedibili, deviano il trasduttore dal suo comportamento lineare (le misure dovrebbero disporsi allineate).

Errore massimo: è la differenza tra la misura ideale e la corrispondente misura sulla retta dell'errore minimo/massimo.

Precisione: fornisce indicazioni sull'accuratezza della misura nell'intervallo di funzionamento.

Precisione = $\frac{E_{\max}}{Fondo scala}$ ·100 [%]

Il coefficiente di conversione.

Un trasduttore ha lo scopo di fornire un'indicazione proporzionale alla grandezza da misurare. L'uso della retta ideale per calcolare la misura della grandezza di ingresso a partire dalla misura della grandezza di uscita è un metodo poco pratico nelle applicazioni: si dovrebbe determinare l'ascissa corrispondente a un valore misurato che si trova sulle ordinate. Però, dato che una retta è descritta da un'equazione di 1° grado della forma y=m·x+n, dove y è il valore misurato e x è il valore da misurare, si può usare il valore di m e di n per ricavare la corrispondenza cercata:

x =(y-n)/m.

Nell'espressione della retta m è detta pendenza perchè fissa l'inclinazione della retta, mentre il suo inverso (1/m) è detto coefficiente di conversione perchè permette di passare dal valore misurato, ad esempio la lunghezza della lamina dilatata dal calore, al valore da misurare, ad esempio la temperatura della lamina.

In realtà, se si eseguissero una serie di rilevazioni, sarebbe estremamente improbabile che i punti sperimentali si sovrappongano esattamente alla retta ideale. Le cause di questo scostamento possono addursi a:

errori sistematici: ovvero disturbi della stessa natura della grandezza da misurare che si confondono con essa e sono una conseguenza del metodo di misura. Questi errori si presentano inevitabilmente (sistematicamente) ogni qualvolta si esegue una misura e non si possono eliminare; però poichè se ne conosce la causa possono essere calcolati e usati per correggere il risultato della misura.

Ad esempio per misurare l'intensità di corrente che scorre lungo il ramo di un circuito, si inserisce l'amperometro in serie. L'indicazione data dallo strumento sarà errata, perchè esso con la sua resistenza interna va ad aumentare la resistenza del ramo e quindi la corrente che lo attraversa non è più semplicemente I = V_ab/R, ma diventa I' = V_ab/(R+r_s). Questa deviazione dal valore corretto si verifica ogni volta che si ripete la misura, si tratta cioè di un errore sistematico.
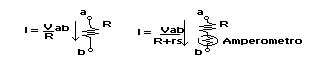
errori accidentali: sono dovuti a disturbi imprevedibili che per cause indesiderate, si possono sommare o sottrarre dal valore vero della misura. Ad esempio nel misurare la corrente lungo un conduttore può succedere che la resistenza del conduttore varia per effetto Joule, o forse lo strumento potrebbe essere sensibile al campo magnetico terrestre e quindi a seconda della direzione in cui si trova può falsare la misura, o magari lo strumento potrebbe risentire dell'inclinazione del piano su cui è posto o all'intensità della luce o ad altre cause. Nel loro complesso tutte queste cause perturbatrici introducono una quantità enorme di errori incontrollabili. Quindi, se si effettua una misura, pur adottando tutte le precauzioni per ridurre le cause di errore, è estremamente improbabile che nel ripeterla si ripresenti lo stesso identico valore. Ci si chiede allora quale risultato bisogna accettare come valore della misura che si effettua. Visto che non vi sono motivi per scartare un risultato, in quanto non si conosce mai l'entità degli errori accidentali che intervengono ogni volta, si rinuncia alla speranza di determinare il valore vero della grandezza da misurare, e si ricerca il valore più probabile che essa può assumere. Il procedimento sperimentale consiste nel ripetere la misura un gran numero di volte e di accettare, come valore più probabile, il valore medio di tutte le misure.
Lettura dello strumento. Con un normale strumento di misura è difficile osservare la presenza di errori accidentali. Il costruttore dello strumento conoscendo la posizione dello 0, come posizione di equilibrio dell'ago indicatore, e quella di fondo scala, ottenuta con una misura campione, suddivide l'intervallo di escursione dell'ago dello strumento in N parti, nel limite dell'incertezza dello strumento, e le numera. Egli assume che lo strumento si comporti regolarmente su tutto il suo intervallo di funzionamento. L'ampiezza risultante delle suddivisioni tiene conto delle limitazioni costruttive dello strumento: inerzia, attriti, gioghi ecc.. dei meccanismi interni. Automaticamente resta fissato il numero di cifre con cui si può eseguire una lettura.
Ad esempio se il fondo scala è 100, e il numero di suddivisioni è 25, risulta un'ampiezza di ciascuna divisione pari a 4 unità di misura. Cioè esisteranno le gradazioni 0, 4, 8, 12 ecc.. e sarà possibile stimare la posizione della lancetta, all'interno di una divisione, con un'accuratezza che non può essere inferiore a mezza gradazione (che in questo caso è 2).

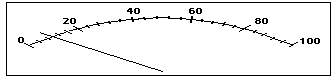
Si potrà individuare la posizione della lancetta dicendo che è compresa tra 8 e 10, ma non ci si potrà spingere a tentare di affermare che la sua posizione precisa è 8.957, perchè le cifre a destra delle unità non vengono fornite dallo strumento preso ad esempio. La misura pertanto va letta così come indicato, oppure dicendo che essa è 9 ± 1.

Parametri dei trasduttori.

Il costruttore caratterizza le prestazioni del trasduttore mediante parametri che riepilogano le osservazioni sperimentali. La relazione ingresso-uscita del trasduttore è rappresentata da una retta. Le misure sperimentali ripetute un numero elevato di volte, a causa degli errori accidentali, si dispongono ai lati della retta ideale.

La misura che presenta il massimo scostamento dalla retta ideale consente di ricavare l'errore massimo della misura; sebbene esso si sia potuto presentare in corrispondenza di una sola misura e magari per una sola volta, non ci sono ragioni per escludere che si possa ripresentare in corrispondenza di uno qualsiasi degli altri valori. Cioè, non conoscendo la causa dell'errore, si deve estendere a tutto l'insieme delle misure la possibilità che esso torni a presentarsi: si tracciano due rette parallele alla retta ideale, una per il massimo errore ed una per il minimo errore, per delimitare la zona entro cui si possono osservare le misure reali.

precisione

È l'errore massimo che si può presentare riferito all'intervallo di funzionamento del trasduttore, detto Fondo Scala.

La precisione dà un'indicazione sull'affidabilità della misura nell'intervallo di funzionamento del trasduttore. Una conseguenza immediata della definizione di precisione è che l'errore su una misura può essere reso tanto più trascurabile, quanto più l'indicazione dello strumento si avvicina al fondo scala.
Risoluzione.

Rappresenta la minima variazione che deve subire la grandezza da misurare per riuscire ad osservare una variazione nell'indicazione dello strumento.

Per comprendere il concetto di risoluzione si pensi ad un comune orologio munito delle lancette per le ore i minuti e i secondi, se con esso si misura l'intervallo di tempo che un corpo impiega per percorrere, a velocità di 10m/sec, la distanza di 300m si otterrà l'indicazione di 30sec. Ma questa indicazione si avrebbe anche se la distanza fosse di 309m, perchè l'orologio non possedendo la cifra decimale per indicare 30.9sec, continuerebbe ad indicare 30sec. Mentre se la distanza diventa 310m, allora l'orologio segnerà 31sec. In questo caso la risoluzione dell'orologio è di 1 secondo, perchè è la variazione minima della durata di un fenomeno che può essere rilevata dall'orologio.
Sensibilità.

È il rapporto tra la variazione della grandezza alterata nel trasduttore e la variazione della grandezza esterna che ne ha causato la trasformazione. La sensibilità quindi è un indice della capacità del trasduttore di avvertire le variazioni della grandezza da misurare. Ad esempio una bilancia che per ogni peso di 100g fornisce una rotazione dell'ago di 30°, ha una sensibilità di 0.3°/g. Quindi per aumentare la sensibilità si deve cercare di causare un'ampia escursione della grandezza rilevata per una fissata variazione della grandezza da misurare.
linearità.
Quando il costruttore vuole caratterizzare le prestazioni del suo trasduttore mediante l'indicazione della linearità, deve precisare anche il criterio secondo il quale ha scelto la retta ideale; in altri termini si definisce linearità, e si misura in percentuale, lo scostamento della misura dal comportamento lineare del trasduttore. La difficoltà principale, che impedisce di applicare praticamente la definizione, è che il comportamento ideale, cioè quello nel quale tutte le misure sono prive di errori non è valutabile. Per determinare la retta ideale si può scegliere tra due metodi:

1. si congiungono con una retta le misure agli estremi dell'intervallo di funzionamento.

2. con tutte le misure a disposizione si calcola, applicando il metodo dei minimi quadrati la retta che si trova al centro di tutte le misure.

Si calcola lo scostamento massimo Δe delle misure vere dalla corrispondente misura x su tale retta; la linearità è il rapporto (Δe/x) 100.
Isteresi.

È lo scostamento massimo tra due misure della stessa grandezza ottenute però da direzioni opposte. Si pensi ad una bilancia sulla quale si pongono in successione dei pesi da 100g. Al primo peso si leggerà, ad esempio, 100g, dopo avere aggiunto il secondo peso si leggerà 199g, dopo il terzo peso si leggerà 299g e così via. Se adesso si ripetono le letture man mano che i pesi vengono tolti, si potrà leggere 201g in corrispondenza della misura eseguita con due pesi da 100g. L'isteresi, in questo caso, è 2g, ovvero uguale alla differenza tra l'indicazione ottenuta per valori crescenti e l'indicazione ottenuta per valori decrescenti, in corrispondenza di uno stesso valore della grandezza da misurare.
La causa dell'isteresi può essere attribuita a diversi fattori: in uno strumento, in cui vi sono organi meccanici in movimento, l'isteresi potrebbe essere dovuta agli attriti che le parti incontrano nel loro movimento. La lancetta che passa dalla posizione 100g alla posizione 200g incontra una certa resistenza al moto e viene frenata, ad esempio, nella posizione 199g; analogamente, nel passaggio da 300g a 200g, incontra un attrito (non necessariamente uguale al precedente) che la rallenta e la ferma in posizione 201g.

Interpolazione.

Si possono presentare casi pratici in cui un trasduttore non ha un comportamento rigorosamente lineare, tale da consentire di ricavare con un semplice calcolo il valore dell'incognita associato al valore della misura, come descritto nell'esempio della lamina metallica sottoposta ad una dilatazione termica. Si esamini la seguente tabella di dati sperimentali rilevati da un trasduttore di concentrazione di ossido di carbonio:

C	V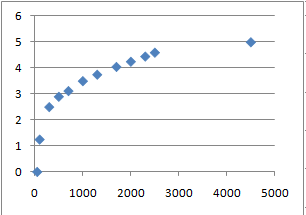
50	0
100	1.25
300	2.50
500	2.90
700	3.12
1000	3.50
1300	3.75
1700	4.05
2000	4.25
2300	4.45
2500	4.60
4500	5.00

Dove V è espressa in Volt e la concentrazione di ossido di carbonio è espressa in parti per milione. Il grafico dei valori riportati nella tabella mostra che la relazione tra la concentrazione e la tensione non è esprimibile tramite una retta. Quindi il metodo pratico di moltiplicare la tensione fornita dal trasduttore per il suo coefficiente di conversione, al fine di determinare la concentrazione di CO incognita, non è applicabile.

Visto che la relazione non è esprimibile tramite una retta, ovvero tramite un'equazione di primo grado, si potrebbe tentare di approssimarla tramite una parabola (un'equazione di secondo grado). Il metodo dei minimi quadrati consente più in generale di determinare un polinomio di grado n che approssima i punti sperimentali.

Semplicemente, si può ammettere che i punti sperimentali siano congiunti da segmenti, ed accettare l'approssimazione che così si introduce. Il procedimento di interpolazione consiste nel calcolare una concentrazione di CO incognita, assumendo che il trasduttore si comporti linearmente nell'intervallo tra due misure note. Ad esempio si calcoli la concentrazione di CO supponendo di leggere, sullo strumento, il valore 3.00V.

Osservando la tabella si vede che si conoscono i valori di concentrazione relativi ai valori 2.90V e 3.12V.

In base all'assunzione che i due punti sono congiunti da un segmento di retta, allora il punto intermedio deve essere allineato con essi, e per la similitudine tra i triangoli:

\frac{V_{2} - V_{1}}{{V - V}_{1}} = \frac{C_{2} - C_{1}}{C - C_{1}}

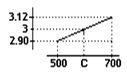da cui:

C = 500 + \frac{3 - 2.90}{3.12 - 2.90} (700 - 500) = 590 ppm

L'estrapolazione.

Si supponga di rilevare una misura V = 5.12V, esterna all'intervallo in cui sono note le misure. Il procedimento di estrapolazione consiste nel supporre che il trasduttore continua ad assumere un comportamento lineare, al di fuori dell'intervallo delle misure, che è il proseguimento dell'ultimo segmento tracciato.