Metodo di Newton.

Si sceglie un valore qualsiasi x₀ di x e si ammette che sia una soluzione.

In tale punto si calcola il valore della funzione e il coefficiente angolare della tangente alla funzione in questo punto.

Il coefficiente angolare della tangente alla curva della funzione f(x) nel punto x₀ è:

m = $\frac{{f(x}_0)}{x_0-x_1}$

In questa espressione ci sono due incognite: m il coefficiente angolare della tangente e x₁ il punto dell'asse delle ascisse intersecato dalla tangente alla funzione nel punto x₀.

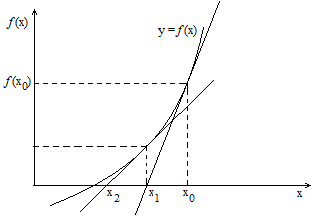
Il metodo di Newton consiste nel calcolare il coefficiente angolare della tangente, con una certa approssimazione, ovvero si calcola la pendenza della corda che taglia la funzione in due punti molto vicini tra loro: x₀ e x₀+h. La pendenza di questa corda è:

m₁ = $\frac{f(x_0+h)-f\left(x_0\right)}{h}$

Ammettendo che i due coefficienti angolari siano uguali, m = m₁, si ricava che la tangente interseca l'asse delle ascisse nel punto:

$x_1=x_0-\frac{f\left(x_0\right)}{m_1}$

Il punto x₁ così calcolato viene usato per tracciare una nuova tangente e nel calcolare una nuova intersezione con l'asse x. Il procedimento si ripete fino a quando si trova un punto x in cui f(x) è minore di una prefissata approssimazione.

L'algoritmo potrebbe non convergere, nel qual caso il ciclo non si arresterebbe mai. Per imporre un limite massimo, oltre il quale ammettere che non esiste la soluzione, si finna un numero massimo di tentativi.

diagramma di flusso

Algoritmo

Codificare il seguente algoritmo

#include <cstdlib>
#include <iostream>

using namespace std;

dichiarare una funzione Newton che restituisce un double e riceve un parametro di tipo double.

double Newton(double x) {
  return x*x-36.0; // si cerca la radice di 36
}

int main(int argc, char *argv[]) {

dichiarare le variabili di tipo double: x, h, f1, m1;
   
scegliere un valore, in formato float, 
        che sia compreso nell'intervallo 
        di definizione della funzione,
        vicino alla soluzione,
        e assegnarlo alla variabile x,
        si ammette che x sia una soluzione.

scegliere un valore molto piccolo rispetto al'intervallo 
        che comprende la soluzione e il punto che si è
        ipotizzato che sia una soluzione
        e assegnarlo alla variabile h

Calcolare la funzione nel punto x e assegnare
        il risultato alla variabile f1

ripetere:
      calcolare m1 secondo l'espressione indicata sopra

      calcolare il nuovo valore di x: 
                    l'intersezione della tangente con l'asse x
                    secondo l'espressione per il calcolo di x1 indicata sopra.
      
      calcolare il valore della funzione in questo punto ed assegnarlo ad f1
fintantochè f1 > h

stampare il valore di x (la soluzione cercata).
}

Esercizi

Calcolare e stampare il numero di iterazioni svolte per raggiungere la soluzione

Confrontare il numero di iterazioni dei due metodi (del dimezzamento e di Newton)

Cambiare il valore iniziale assegnato alla x e utilizzare le modificiche precedenti per controllare il numero di iterazioni occorrenti per raggiungere la soluzione